Magic Land The swerving rollercoasters round me roared, As I traversed the park myself. Though bored, I stayed near, faithful close as others soared, I was held in place. Leashed, one might say, And circumspect, a vacation hemmed in By the limitations of a declining constitution And plunging mortality. I ruminate grimly Among the strollers, flat-footed and benched. But as I take in the three-ring circus — A sandbox carefully drafted and sculpted Into existence by a host of Imagineers, I, like a near-sighted country pulpiteer, Can’t quite grasp the stained-glass epiphanies, But divine the carnie colors of the pulped revival. From my perch I can radially behold The fathers strapped into papooses, kids Darting ahead in wholesome happiness and criminal conniving, Moms with maps, couples in matching mouse ears, young Adults hidden in hothouse suits, scrambled I’m sure By the relentless rays of the noonday sun, so much rodeo Within my range, clowns and bulls and cowboys And the motes of dust kicked up and settling, Floating and whizzed around in turbulence, plunging Irrationally, a perfectly chaotic vertigo…
Honoring Interests
This is hard to do. Kids are often interested in stuff that seems weird, mundane, or inane to us. They make things that generally qualitatively bad. It’s hard to be enthused about stories that seem pointless, art that seems ugly, insights that seem pointless, thoughts that seem bizarre.
But the best encouragement we can give is our attention. We need to see profferings as mustard seeds of creativity, empathy, acuity, and articulation. If we want them to find delight in craft and language and logic and work and beauty, we’ve got to stoke their fledgling enthusiasms.
That’s why we pin art to our refrigerators. Feign surprise at their tales. Repeat to our spouses their discoveries at the dinner table.
That’s why, when they give us a pocketful of unremarkable pebbles they collected on our walk, you display them as if in a museum.

Body Art
I like to encourage my youngest to write, draw, and scribble. We’ve established walls, floors, and furniture are off-limits (at least I think we have), but I don’t really have a problem with him drawing on his own body.

Logic of English
I’ve started the Logic of English curriculum, which primarily benefits the 4-year-old. I’m subjecting the 7-year-olds to it as well, though, in order to give them more systematic cursive writing instruction. I like how LOE combines handwriting with phonics, and am convinced that its approach to phonics is more comprehensive and logical than other curricula I’ve seen. I think it’ll make spelling and comprehension easier down the road.

I’m not one to buy curricula whole-cloth, and LOE is not inexpensive, but I’ve found Denise Eide’s presentations persuasive (she’s the creator of the program). You’ll also find on the web site free training modules and samples that will give you a good idea of what the curriculum entails.
Random Walks
To add a little variety to our walks, I’ve introduced a little randomness.
I downloaded an app for my phone that generates a random option — there’s a ton of them out there — and set options for “left,” “right,” and “straight.”
I tried it out today. It was bitter cold — the first real test of our resolve to keep up these walks, no matter the weather — and the kids had their hackles up. But they were mildly intrigued at the suspense of our path. Every time we got to an intersection, I pulled out the app and let it determine our next move.
It was a short walk, but it was a new walk for us. When we got back, I made hot cocoa for everyone.

Shape Chain
Cut out shapes from construction paper. Talk about them, name them. Punch a hole in them, and string them through twine.

Set
Great game that practices recognizing patterns. My seven-year-old can not only play the game but frequently beats me. My three-year-old doesn’t quite understand what a “set” is but likes to compare and contrast cards.
You can also solve daily Set challenges online.

Headspace Guide to Meditation
We normally have an afternoon “quiet time,” a half hour during which you must be alone and quiet. Recently, though, I’ve substituted this quiet time for watching 20 minute episodes of the “Headspace Guide to Meditation” on Netflix.
I don’t think meditation is a substitute for prayer, and I don’t treat it like a spiritual discipline. I do, however, consider it a useful tool that helps defrag one’s neurology.
Hopefully, the kids might consider it a skill worth resorting to in future quiet times.
This week in Math Madness: Planar Shapes & Mobius Strips
We started off this week going back to some of the Eulerian circuits we worked on last week and tried out Euler’s Formula on them.
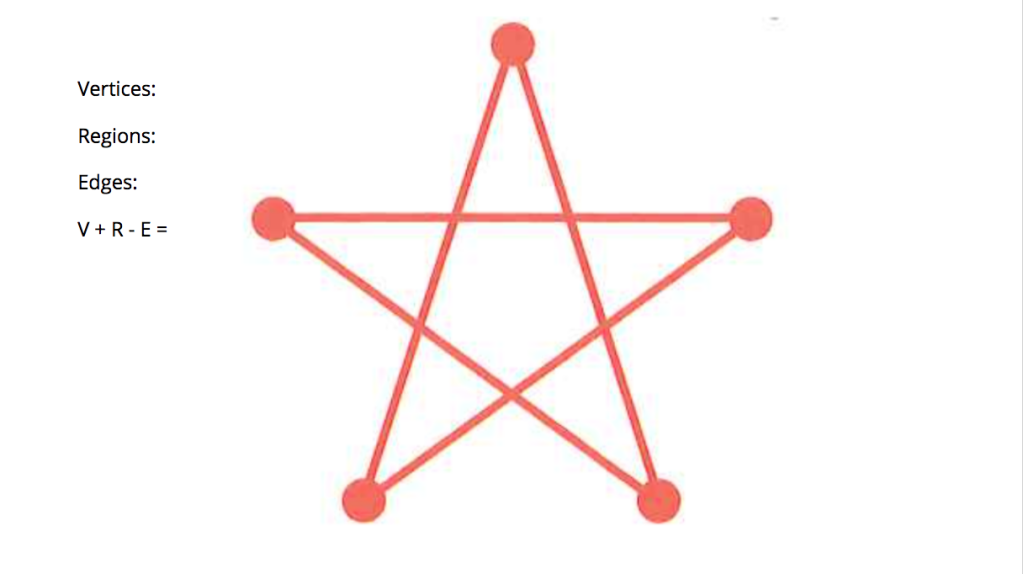
After defining what vertices, edges, and regions are, as defined in graph theory, we counted up those elements in each of the shapes and found that the sum of the number of vertices and edges minus the number of regions always equaled two.
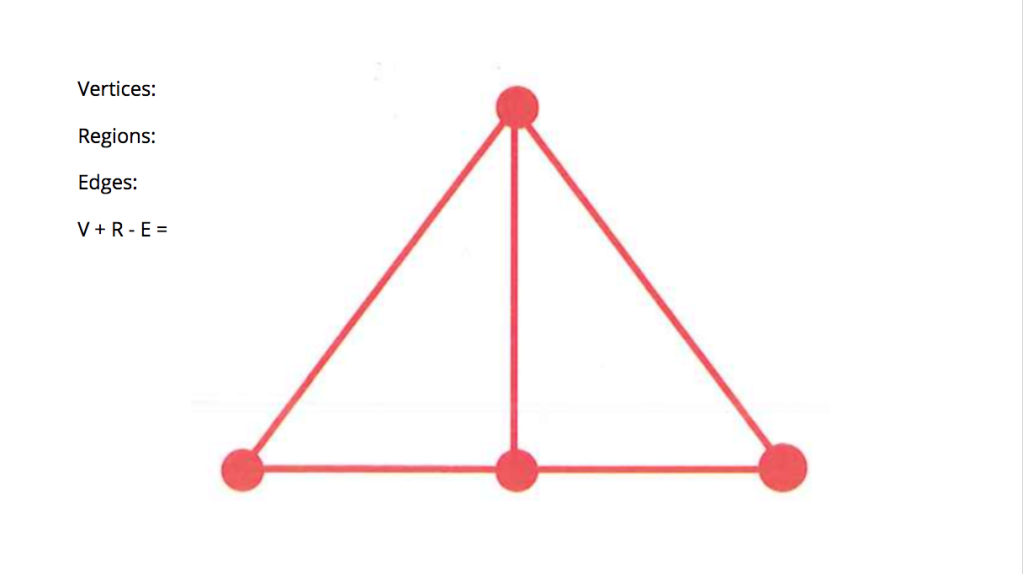
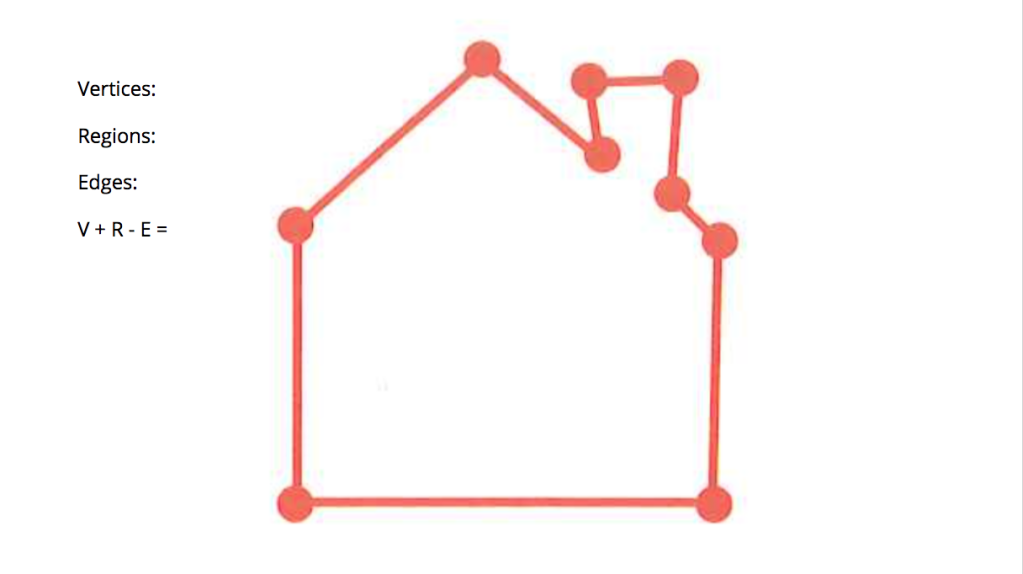
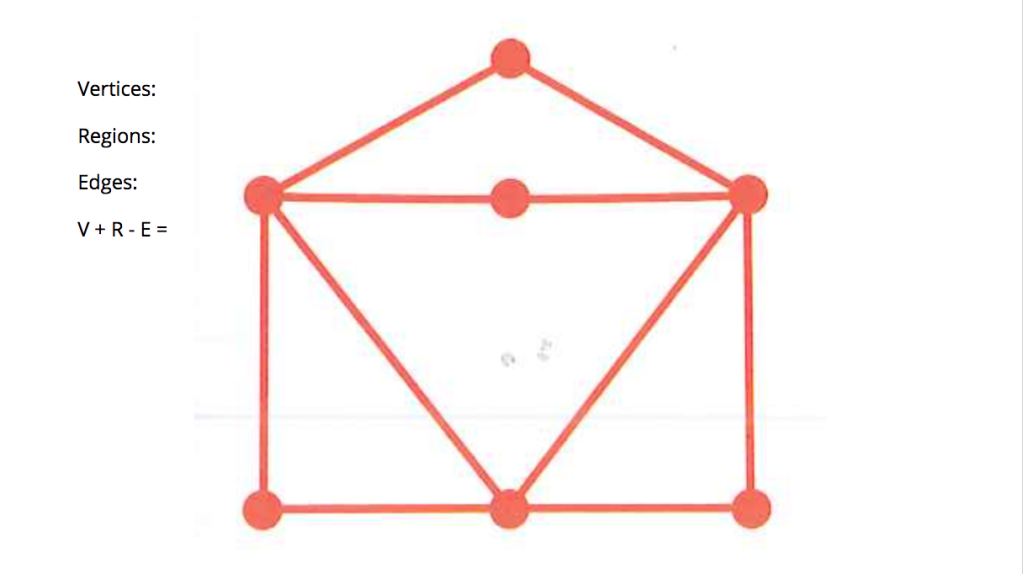
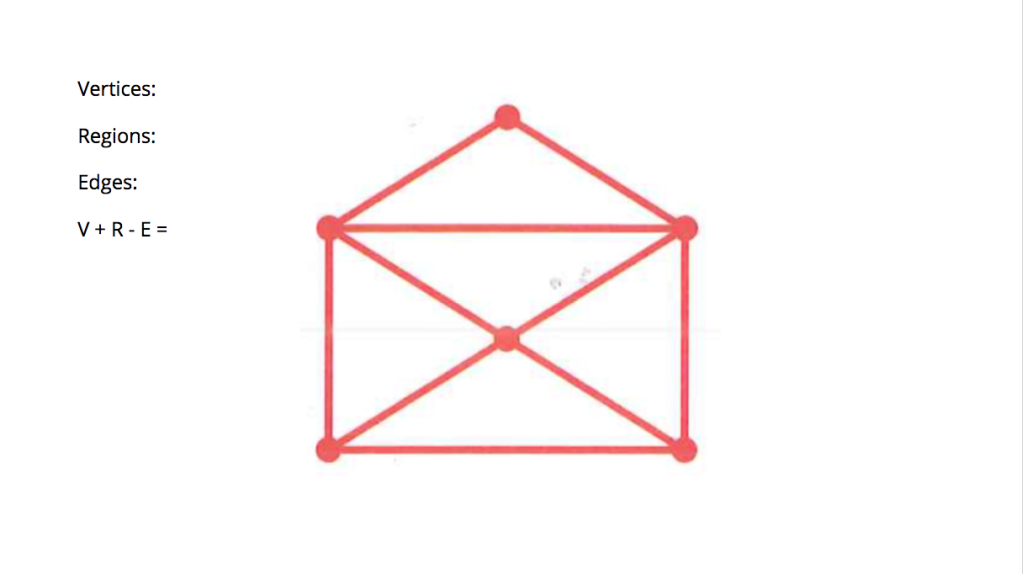
We found, though, that this only worked if we followed a couple of strict rules.
This star, for example, doesn’t work:
But if we make it planar (edges can’t cross without vertices), it works out:
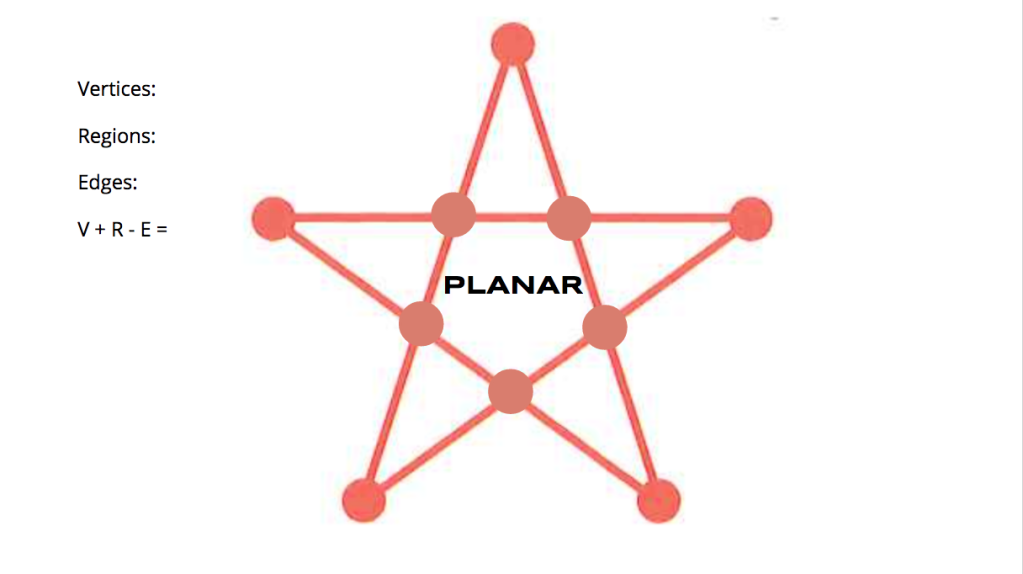
Similarly, every edge needed at least one vertex:

And only one figure at a time. Not this:

But this is okay:

Most of these exercises were taken from Math Lab for Kids by Rebecca Rapoport and were designed by Fan Chung.
I mentioned this is all a branch of mathematics called topology. Most people, when they think of topology, think of Mobius strips. Much to my excitement, most of our Mad Math-ers hadn’t heard of them!
We first saw this clip of Avengers: Endgame that featured a Mobius strip:
And then we made a regular loop from a strip of paper. Then a loop with a half-twist (Mobius strip). Then a loop with a full twist. We saw the former and latter loops had two sides. The Mobius strip only had one. (!!!)
We then cut each of the loops in half. The first loop divided into two separate loops. The loop with the full twist separated into two intertwined loops (of the same size). The Mobius strip just divided into one loop of double the size.
We then watched the following video of Vi Hart and emulated what she was doing:
She mentions a lot of interesting things, but I was able to talk a little bit more about rotational symmetries, frieze patterns, and glide symmetries so that we could follow what she was doing.
I strongly encourage anyone to experiment with Mobius strips, either with paper strips or with fruit leathers! They have such counter-intuitive properties that don’t really make sense until you think of them mathematically.
A little bit of extra credit. Before Avengers: Endgame was released in theaters, this gentleman had a theory about how the movie could utilize time travel in interesting ways using Mobius strips. If the dimension of time was a Mobius strip, you could resolve time-traveling paradoxes with something like quantum superpositioning! This ultimately wasn’t the direction the movie went in, but mind-blowing all the same:
Homeschool Ergonomics
I recently listened to a Life Kit episode (NPR) about ergonomic issues around remote working or learning. Their expert advisor was Meg Honan from the Department of Occupational Medicine at University of California San Francisco — their web page on the topic is full of good stuff.
Here’s a quick bulleted summary:
- Lift your head and lower your arms
- Top of monitor should be at eye-level
- Helps: laptop wedge or external monitor
- Keyboard/mouse at resting elbow level
- Otherwise hunched over and lifting arms (like praying mantis)
- Most desks/tables too tall
- Raise height of chair or sit on pillow
- Keep feet flat, though, to support lower back
- Find platform/footrest for feet if don’t reach floor
- Pillow at small of back also helps with lower back
- Keep feet flat, though, to support lower back
- Raise height of chair or sit on pillow
- Helps: detached mouse/keyboard
- External mouse also avoids ergonomic problems with trackpad
- “Heads down, arms up” position makes you achy, sore, tired
- Top of monitor should be at eye-level
- Switch positions
- Don’t stay in one position for too long
- Use new tasks to move around and adopt a new posture
- Walk around during calls
- Play breaks/Brain breaks
- Break up your day with walks, stretches, etc.
- At least once per hour
- Get fresh air and sunshine
- Balance 2D screen time and 3D work
- crafts, chores, games, etc.
- Use new tasks to move around and adopt a new posture
- Don’t stay in one position for too long
- Keep consistent structures/routines
- Get buy-in and input from everyone involved
- Invest time and effort to get and stay organized
- Rotate activities to help maintain motivation
- Set goals; keep to-do list
- Work on one thing at a time
- Eliminate distractions
- Be kind to eyes
- Avoid glare: Sit perpendicular to window
- Good lighting
- Adjust screen brightness
- Use max screen space
- Watch lecture/lesson AND take notes on a separate surface
- Project onto TV screen (smart TV/Apple TV)
- Consider ears
- Headphones (with microphones)
- Don’t blast volume
- Decrease background noise
- Pay attention to discomfort
- If discomfort/pain lingers for days, or builds, it could be serious
- You’re a person, not a product
- Socialize with friends, family, colleagues regularly
- Create wellness boundaries
- e.g., no tech during meals
It’s made me reflect on the homeschooling space I’m planning for the new home. It’s connected to a screened-in porch because we wanted to encourage the kids to go outside as much as possible. Along those lines, we want to put in enticing or interesting features within direct visibility from the porch — perhaps a mud kitchen or a hammock or a vegetable garden or game equipment. The porch area would also be handy for messy activities like art or science experiments.
I’ve decided not to give individual kids their own desk in the homeschool space. Instead, there will be a central table (at the proper height for working, not eating) and learning stations at edges and corners of the room. I can vary the furniture so that some spots encourage standing while other spots encourage other postures, like playing on the floor or reaching up to a shelf. I’d like to put a computer at standing height for the younger ones in one corner of the room, but I’d also like to set up a cheap projector to project the computer screen onto a blank wall.
I’m also going to try to minimize clutter in the room by paring down the materials visible and available. There will a couple perennial supplies — pencils, paper, glue, and so on — but I’ve been inspired by Montessori classrooms to keep a clean, minimal aesthetic and rotate out activities and supplies.
I try not to get sucked into Pinterest vortices, but I’ve drawn a lot of inspiration from Tinkerlab and Fairy Dust Teaching.
